今回は統計的検定の一つマン・ホイットニーのU検定[1]を言語データの分析に利用する方法を紹介します。
この記事は「言語學なるひと〴〵 Advent Calendar 2023」の10日目として書かれました。1日遅くなってすみません…
[1]多くの統計的検定が「[開発者の名前]+[使用する統計量]+検定」というような名前をとります。今回の場合はマンさんとホイットニーさんが作った、Uという統計量を使った検定、ということです。
目次
はじめに
閻・堤(2023)や『計量国語学』における「言語統計学入門」の連載など、最近では日本語研究者のための統計学の入門書がどんどん充実してきています。ある分析/検定方法について学んでも、それを実際に目の前のデータに利用する段階が意外と難しかったりするので、特に言語データについてこうした入門書があるのは本当にありがたいです。
ですが、これらの本は検定について言えばスチューデントのt検定のような平均値の検定とペアソンのカイ二乗検定やフィッシャーの正確検定のような比率の検定について扱っているものが殆どで、順序尺度に適用できるマン・ホイットニーのU検定については触れられていないことが多いです。入門書としてよく使う検定が選ばれているということなんだと思いますが、個人的にはいやいやマン・ホイットニーのU検定も結構使いますぞと思うのです。
そこで今回はマン・ホイットニーのU検定が具体的に言語データの分析にどんな風に利用できるか出来る限り簡単に説明して、以てその知名度アップを目指すことにします 。
今回は統計に詳しくないという方にも興味を持って読んでいただけるように、可能な限り直感的な説明に努めます。このことによる不正確な表現/語弊を予めお詫びいたします。そもそもこのような記事を書くのは自分では力不足な気もしていますが、可能な限り正確で簡易な記述になるよう精一杯頑張ります。
統計的検定とは
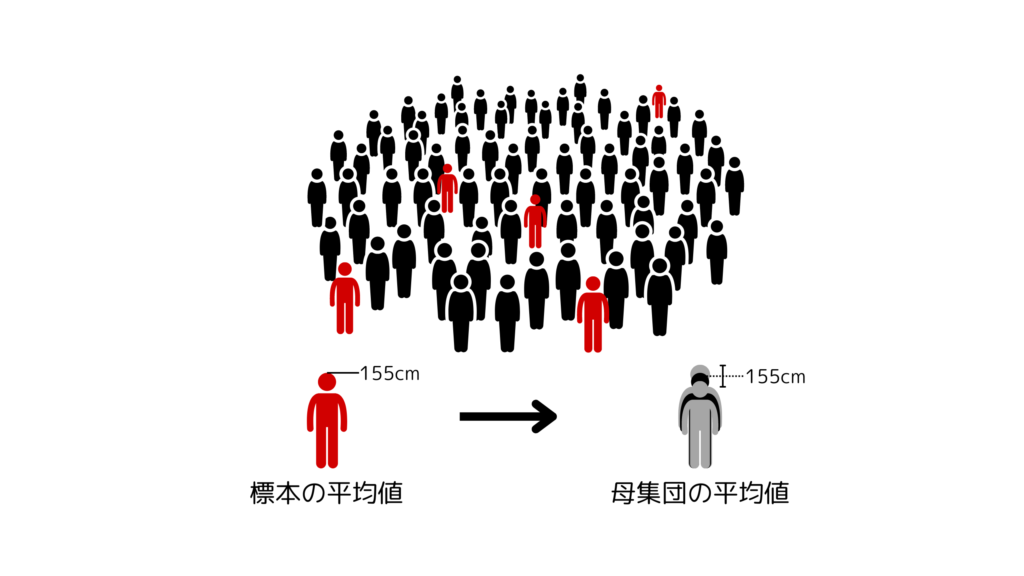
ある程度大きな集団について調査を行うとき、その全てを調査するのは大変ですから、一部分(標本といいます)だけを調査してその結果をもとに、集団全体(母集団といいます)の様相を推測するという方法がとられることがあります。3年A組の身長を10人だけ測ったら平均が155cmだったので、全員分測って平均を求めても大体そのくらいになるだろう、といった感じです。そんなこと本当に言えるのか?と思ってしまいますが、ある程度の誤差を認めて[1]、誤った判断をする可能性[2]もある程度許容すれば、そのように言って大丈夫!ということになっています。
以上のような方法のうち、統計的検定とは母集団に関する仮説が支持できるかどうかを標本をもとに決定する手続きです。もっと具体的に言うと「Aの集団とBの集団に本当に差があるといえるのか(偶然じゃないのか)」ということを決定するものです[3]。
ここで少々トリッキーなのが、支持できるかどうか判断したい仮説の確からしさをそのまま求めるわけではないということです。とっても語弊のある書き方になってしまいますが、まずは多分違うだろうなと思う仮説(帰無仮説といいます)の確からしさを求め、それが十分低ければ、それと対立するところの本命の仮説(対立仮説)を支持することができるという仕組みになっています。
差の検定では、まず二つの標本が同じ母集団から得られたものだと仮定します[4]。これを帰無仮説と言います。どうやら差がありそうだなと思っていても、というか思っているからこそ、まずは差が無いと仮定します。
そうすると、二つの標本が同じ母集団から得られたものなんだから、当然それぞれの標本から推測される母集団の平均値も同じだろうし、分散も同じだろうし…という具合に色んなことが導けます。

あとはこれらの条件を上手く使って、標本が目の前の値をとる確率を求めます[5]。これが十分低ければ、仮に二つの標本が同じ母集団から得られたとしたら標本がこんな値をとる可能性はほとんどない、ということになって、それじゃあ、やっぱり最初の仮説が間違っていたんだろうから、逆に二つの標本は別の母集団から得られたんだろうという仮説(対立仮説)が支持されるわけです。
[1]許容誤差と言います。
[2]有意水準や有意確率と言いますが特にこの意味では危険率と呼ばれます。
[3]これは特に、差の検定の説明です。
[4]標本を同じ確率分布関数に従う確率変数だと仮定するということ。
[5]まさにこの「上手いこと確率を求める方法」が盛んに研究されて、現在までに様々な検定が提案されているわけです。
変数の尺度
統計的検定の過程において帰無仮説から得られる様々な条件を上手に使って目の前の結果が得られる確率を求めると書きました。このとき当たり前ですが、対象とするデータによって計算の方法が異なります。データ(変数)の性質や母集団に関する前提、標本の数、対応の有無など利用できる様々な条件が異なるからです。
今回はこのうちデータ(変数)の性質についてのみ説明します。データ(変数)はその性質によって以下の4つに分けることができ、それぞれ可能な演算が違います(Stevens, 1946)。
| 名義尺度 | 変数間の異同を示す尺度 | =, ≠ |
| 順序尺度 | 変数間の順序を示す尺度 | =, ≠, >, < |
| 間隔尺度 | 変数間の差を示す尺度 | =, ≠, >, <,+,- |
| 比率尺度 | 変数間の比を示す尺度 | =, ≠, >, <,+,-,×,÷ |
そのため、使用できる統計量も勿論異なってきます。たとえば間隔尺度以上であれば平均値や標準偏差を求めたりすることができますが、名義尺度では足し算も割り算もできないのでそれができません。[猿、猿、猿、犬、犬、きじ、きじ、きじ]のようなデータの平均値なんて計算できないですよね。
ということは勿論、使用できる検定も異なってくるというわけです。スチューデントのt検定は平均値を使いますから[1]、間隔尺度以上にしか使えませんし、逆にペアソンのカイ二乗検定は比率が分かればいいだけなので、どんな尺度にも使える[2]、という具合です。
[1]加えて二つの母集団が同じ分散であること仮定する必要があります。またデータの対応の有無によって計算方法が異なります。
[2]とはいえ、名義尺度以外のものに使うことは少ないです。名義尺度以上のものを名義尺度としてあつかうと言うことはその分情報を無駄にしていることになります。また期待値が小さい場合にはカイ二乗値のカイ二乗分布への近似がよくないので、推奨されないことにも注意が必要です。
マン・ホイットニーのU検定
マン・ホイットニーのU検定は簡単に言えば、順序尺度以上のデータに対して二つの集団の大きさを比較する検定です。魅力的なのは順序尺度以上であれば基本的にどんなデータにも使えるというところです。
手順
ほとんどの統計ソフト[1]に入っているので、実際にはパソコンに任せることが多いですが、小標本の場合には簡単に手計算することができて、何をやっているのかが分かり易いので一度計算してみることをおすすめします。
具体的には以下のような手順で求めます。
- 変数を順番に並べる
- 一方の群に注目して、それぞれのデータより大きいデータがもう一方の群にいくるあるのかを数えて、結果を合計する(これが統計量U)。
- 2.の結果をUの分布表[2]と照らして確率を求める。
- 帰無仮説を棄却/受容する。
もっと詳しく知りたい方にはこちらの記事がおすすめです。
言語データとマン・ホイットニーのU検定
さて、ここまでで説明が随分長くなってしまいましたが、やっと本番です。マン・ホイットニーのU検定が、言語データの分析にどのように使用できるか見ていきます。
言語形式×変数
言語形式はほとんどの場合名義尺度[3]ですから「ある集団の間の言語形式の差」を比較する方法はカイ二乗検定やフィッシャーの正確検定のような名義尺度の検定に限られることになります。
ですが、何らかのデータを言語形式によって分けて「言語形式間のデータの差」を比較するのなら、その変数の尺度に応じて使用できる方法は様々あるということになります。「変数の尺度に応じて検定があるのだから、そんなの当たり前だ!」と言われそうですが、検定を勉強したのに言語データにどうやって適用するのか分からないという躓きの多くは、ここの区別ができていないということから来ているように思います。
さて、言語データに対してマン・ホイットニーのU検定を使用するというのも、後者の類いでして、正確には言語形式によって分類された何らかの順序尺度に対して検定を行うということになります。言語形式と何らかの順序尺度が密接に関わっていそうな現象に対して、形式の間に本当に差はあるのかを決定するわけです。
そのため、マン・ホイットニーのU検定を適用できるのは、ずばり「言語形式と何らかの順序尺度が密接に関わっていそうな現象」ということになります。以下で2つの例について見ていきます。なお例示しているデータは説明のために作ったダミーデータです。
ケース1:文の自然さの判断(容認性判断)
あるインフォーマントにとってある文がどの程度自然かという変数は順序尺度と見ることができます。容認性判断とか文法性判断とかいうと、文か非文かというような二値的な尺度(名義尺度)だ!という意見がありそうですし(筆者もどちらかといえばそちらのタイプ)、そもそも母語話者に均一な知識であるとするなら多人数調査の必要もなくなると思いますが、ここで話しているのは「この言い方、私はちょっと違和感あるな」というようなもっと”緩い”尺度です。「自分も使用するし、適切だと思う>自分は使用しないが不適切ではないと思う>自分は使用しないし、不適切だと思う」というような多肢選択のデータが典型的です。
例えば以下の表2の場合、「んさった」と「んなった」で自然さの判断に差があるでしょうか。
| 文 A | の B | 自 C | 然 D | さ E | 合計[4] | |
| 田中さんもう学校いきんさったで。 | 5 | 4 | 10 | 45 | 40 | 105 |
| 田中さんもう学校いきんなった[5]で。 | 30 | 42 | 30 | 1 | 2 | 105 |
中央値を求めると「んさった」がD、「んなった」がBなので、「んさった」の方が自然であると言えそうです。ですが、この差は偶然得られた可能性があります。本当は「んさった」と「んなった」に差はないけれども、今回は偶々「んさった」は自然で「んなった」は不自然だと考える人が偏って選ばれたかもしれないわけですね。そこでマン・ホイットニーのU検定を行ってみるとp<.001と求まりました。繰り返しになりますが、これは仮に「んさった」と「んなった」に差は無いとすると、こんな結果になる可能性は1%にも満たないということです。そのため今回の結果からは「んさった」と「んなった」に差はあるということが言えます。
ケース2:待遇表現の使い分け
待遇表現の使い分けに関わる様々な変数は順序尺度であることが多いです。例えば年齢や親しさなどです。そのためマン・ホイットニーのU検定を使って本当にその基準に基づいて使い分けがあるのかどうかを確認することができます。
例えば、以下の表3の場合、ナルとサルには素材にとる年齢に差はあるでしょうか。
| 素 A | 材 B | の C | 年 D | 齢 E | 合計 | |
| ○○、どこにおんさる? | 2 | 3 | 3 | 54 | 63 | 124 |
| ○○、どこにおんなる? | 1 | 4 | 2 | 65 | 59 | 131 |
サルは中央値がEで、ナルは中央値がDなので、もしかするとサルの方がナルよりも年齢の高い人に使うと言えるかもしれません。ですが、この差は偶然得られた可能性があります。本当はサルとナルで差はないけれども、今回は偶々、サルの方がより年上の人物に使用できるという回答が多かったかもしれないわけです。では早速マン・ホイットニーのU検定をしてみましょう。結果はp=. 485でした。仮にサルとナルに差は無いと仮定したときに、こんな結果になる可能性が50%くらい存在するわけです。そのため今回の結果からはサルとナルに差があるとはいえません。
待遇表現は個人間で使用にズレがありながらも、集団において大体の待遇価が共有されています。そのため、その体系の把握にはこのような検定によって使い分けの差がはっきりあるものと、ほとんど使い分けの差がないものを区別することが有効だと思います[6]。
[1]統計的な手続き(に含まれる煩雑な計算)を自動で行ってくれる研究者の強い味方です。最近では無料で使用できるものも多く公開されています。
[2]統計量Uは帰無仮説下においてその分布が明らかにされています(Mann & Whitney 1947)。
[3]敬語はひょっとすると順序尺度と言えるかもしれませんが、その順序が先験的に分かっていたら、そもそも分析する必要がありませんね()
[4]マン・ホイットニーのU検定においてここの合計(横周辺和と言います)は必ずしも同じである必要はありませんが、今回のような場合は全員に2つの質問をすることになるので、形式間で合計は一致しますね。
[5]筆者が研究している但馬方言の素材待遇形式です。本来ナルは-(i)nar-であって、表3のように/ri/に接続するときに限り撥音となるのですが、サル-(i)ɴsar-の類推から、たまにこういう発話も観察されます。
[6]実際にはとにかく形式間には差があるのだということを前提にして微少な差を持って大小関係を推定している研究も多いのですが、このような考えから個人的にはいただけないなぁと思っています。
終わりに
今回は統計的検定の一つマン・ホイットニーのU検定を言語データの分析に利用する方法を紹介しました。拙い説明で恐縮ですが「U検定意外と使い勝手いいやん!」と思っていただけると幸いです。
あと、もしこれを読んでる阪大生がいましたら、来年(2024年)からこの種の勉強会をしますので興味のある方は是非連絡ください(笑)
参考文献
※参考文献というか文献紹介ですね
閻琳・堤良一(2023)『レポート・卒論に役立つ 日本語研究のための統計学入門』くろしお出版.
Stevens, S.S. (1946) On the Theory of Scales of Measurement. Science, 103(2684), 677-680.
Mann, H.B., Whitney, D.R. (1947). On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Annals of Mathematical Statistics,18(1), 50-60.

