「ゼミのDXを進めたい」第3弾。第1弾、第2弾がともに好評のため、調子に乗って、早速第3弾を書いてみました。今回のテーマはずばり機会学習で語形の分類を行うというものです。様々な語形の特徴を上手くつかんで勝手にグループ分けさせるにはどうすればよいのでしょうか。
なお、当初は前半で方法論を解説して後半でGoogleColaboratoryを使った具体的な実装の手順を書こうと思っていたのですが、前半だけでかなり長くなってしまったので、具体的な実装については別の記事にすることにしました。ご了承…
例によって初めに、この記事に書かれている方法を使って最終的にどんなものができるのかを示しておきます。
お断り:
今回の記事の目的はクラスター分析のアルゴリズムや、語形のベクトル化の厳密な解説ではなく、あくまでわかりやすく語形の自動分類の技術にふれてもらうことです。一部、表記や記述が厳密ではない箇所もありますが、ご了承ください。
目次
クラスタリング:k-平均法(k-means clustering)
機会学習の何たるかとか、非階層型クラスタリングの何たるかなどをここで解説できるほどの知識は私にはないですし、記事の目的からもそれると思うのでそういうものはすっ飛ばして早速今回使用するアルゴリズムの紹介から始めようと思います。
k-平均法は与えられたデータを自動的に分類するクラスタリングの一種で、任意の次元のデータセットをクラスター※1の平均(重心)を使用して指定した数のクラスターに分類してくれるものです。
そもそもクラスタリング、つまりデータセットをクラスターに分類するとはどういうことでしょうか。非常に単純化した例として図2)のような2030年に行われた何らかの調査結果について考えてみましょう。点の一つ一つは回答一つ一つに対応し、縦軸は一つ目の調査項目の回答、横軸は二つ目の調査項目の回答をと対応しています。例えば回答Aは一つ目の調査の結果が23、二つ目の調査の結果が87であったため、A(23, 87)にプロットされています。
さて、このままでは点と点との関係がよく分からないですね。ここで図3)のように近い点は同じ色で表示してみましょう※2。随分点と点との関係が見やすくなりましたね。これがデータセットをクラスターに分類するということで、k平均法のような種々のアルゴリズムはこれを自動で行ってくれるというわけです。


何でそんな魔法みたいなことが達成できるのでしょうか※3。その仕組みは意外とシンプルで以下のようなものです。
- 各データにランダムにクラスタを割り振る
- 各クラスタの重心を計算する。
- 各クラスタの重心と各データの距離を求め、各データを最も近い重心のクラスタに割り当て直す。
- 2~3の行程を割り当てられるクラスタの変更がなくなるまで繰り返す。
視覚的には以下のような行程をたどります(Chire, 2017)。3つの色で色分けされているのがクラスタで、その中心にある+印が各クラスタの重心です。回を重ねるごとに既存のクラスタの重心から遠いクラスタが割り当て直され、それに伴って重心の位置も変更していっているのが分かります。
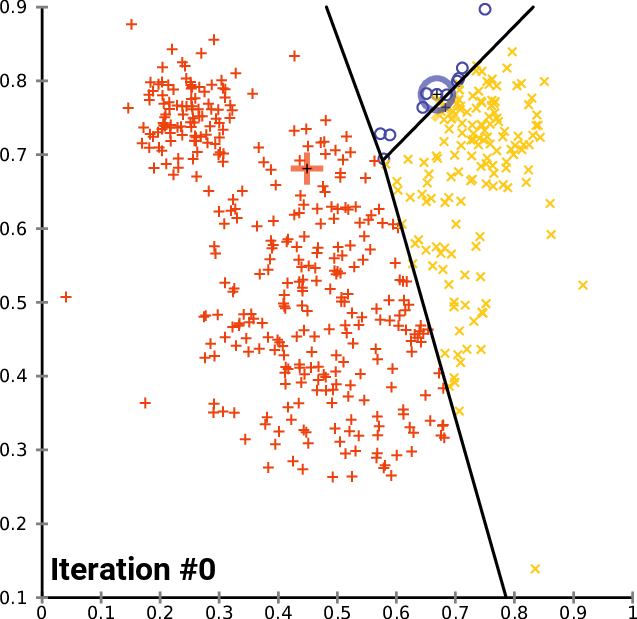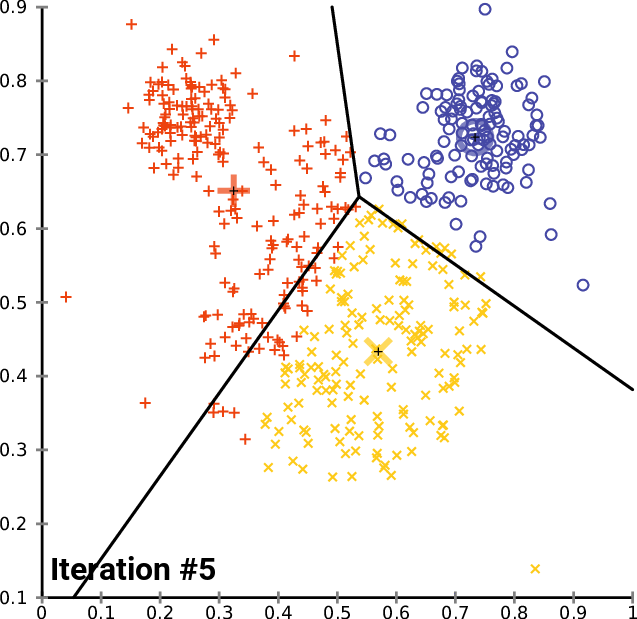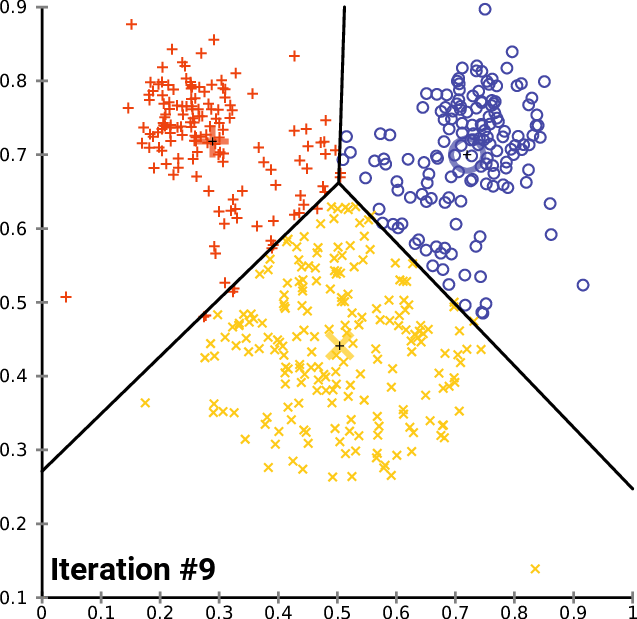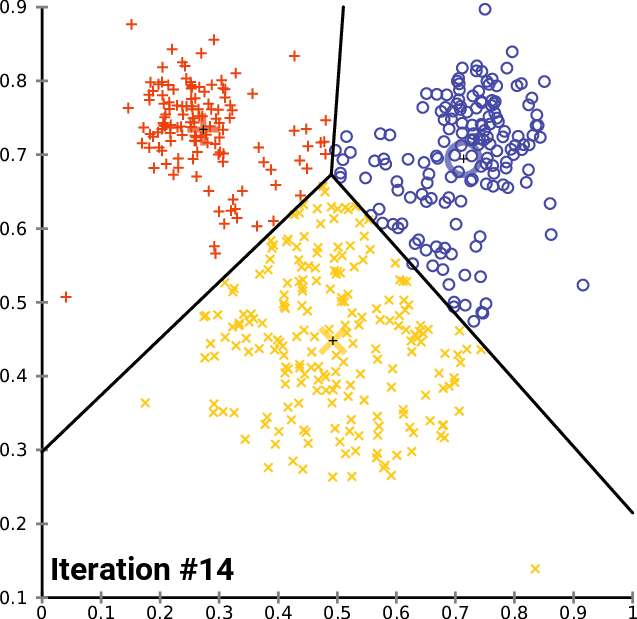
※1ここでは「グループ」と読み替えても問題ないと思います。
※2今回はたまたま近い点は同じグループに属するはずだという仮定のもとグループに分けましたが、勿論別の方法でグループ化することもありえます。
※3仕組みについては他にも色々な記事や動画などで分かり易い解説が提供されていますので、ぜひ「k-means 仕組み」などで調べてみてください。
多次元ベクトル
ここまでで話してきたような任意の変量を持ったデータは多次元ベクトルとして表わされます。
ベクトルとは向きと大きさを持った概念のことで、多次元ベクトルというのはそのような向きがたくさんあるベクトルのことです。(ここで扱うのは特に原点を始点とした位置ベクトルですから、多次元空間の座標と考えてもいいかもしれません。)
実際に例を使って確認してみましょう。表1はA君らのある日のテストの結果を示したものです。(A君がんばれ!)
| 英語の点数 | 数学の点数 | 国語の点数 | 理科の点数 | 社会の点数 | |
| A君 | 50 | 65 | 70 | 44 | 45 |
| B君 | 78 | 67 | 89 | 78 | 90 |
| C君 | 77 | 92 | 78 | 98 | 93 |
| D君 | 92 | 65 | 88 | 96 | 82 |
| ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ |
k平均法を使用するために、これらの結果を図2のように整理するにはどうすればよいでしょうか。図2の場合は調査項目が2つだったために「A(23, 87)」のように縦軸と横軸、2つの軸を使って簡単に回答の結果を示すことができましたが、今回は調査項目が多いのでかなり複雑そうです。が、実際にはそうではありません。今回も図2と同様に調査項目分の軸(向き)を用意してあげればよいのです。「A(50, 65, 70, 44, 45)、B(78, 67, 89, 78, 90)…」という感じですね。
さて、このようなベクトル(或は座標)は見てのとおり3次元以上ですので、これらを図示すること自体は非常に難しいわけですが、このままの状態でも確かに各教科の点数を独立した向きとその大きさとして表わすことができているので目的は達成しています。これさえあれば、以下の様に複数の点の重心をもとめたり、2点間の距離をもとめたりといって、k平均法に必要な計算を十分に行うことができるのです。
語形のベクトル化
前節までで、任意の変量を持ったデータの集合があればそれを上手いこと分類する方法があるということ、そのようなデータの集合は多次元ベクトルの集合として表わされることを確認しました。分類にはまず、分類に適したデータを用意する必要があるんですね。
今回の場合は語形を互いの類似関係が十分表現できるようなベクトルに変換する必要があります。この方法は実に様々なものが提案されていますが、今回はまず(近藤, 2023)による音素ベクトル(BoC)を紹介したあと、それを応用して音韻素性レベルの類似性をも捉えられるものとして素性ベクトル(BoF)を提案してみようと思います(提案というほどのことじゃないけれど)。
音素ベクトル:BoC(近藤, 2023)
従来、語形の類似度を表現するものとしてはレーベンシュタイン距離など色々提案されてきましたが、仮名単位でレーベンシュタイン距離を求めると、あまり上手くいきません。「メダカ」(medaka)と「メタガ」(metaga)とは直感的・語源的にはよく似ていますが、モーラ列としては「メ」以外は一致しないのでレーベンシュタイン距離は遠くなってしまうのです。
そこで(近藤, 2023)では、以下のように各単語に各アルファベットが何回出てきたかという情報を26次元のベクトルに保存するBag of charactersが提案されています。これは音素の特徴量を大雑把に捉えることができるので「コロコロ」と「カラカラ」などの仮名単位では全く別語形である語形の類似性を捉えることができます。
DENDENMUSIの語形音素ベクトル
[ 0 0 0 2 2 0 0 0 1 0 0 1 2 0 0 0 0 1 0 1 0 0 0 0 0 ]
a b c d e f g h i j k l m n o p q r s t u v w x y z
(近藤, 2023)ではこの方法を用いてK平均法で分類することで、日本言語地図の「かたつむり」の類いを「でんでんむし」類「まいまい」類「かたつむり」類のようにある程度分類することができたこと、unigram と bigramとではunigramの方が有効であることが報告されています。
音韻素性ベクトル:BoF
BoCの欠点として、あくまで音素レベルの特徴量ですので両唇音や有声・無声の別といった音素同士の素性レベルの類似性は捉えることができないということが上げられます。例えば「バイバイ」と「マイマイ」のペアが、「バイバイ」と「サイサイ」のペアよりも似ているということは調音点や有声性の情報を参照すれば明らかですが、このモデルでは同様の類似度になってしまうことが予想されます。
この問題を克服するために、今回はすぐに思いつく方法として音韻素性を利用することを考えてみましょう。Aがいくつあるか、Kがいくつあるかではなくて、子音性が陽性である要素がいくつあるのか、口蓋音性が陽性である要素がいくつあるのかなどを数えようということです※2。
実際には一つの音素とローマ字とは必ずしも一対一対応する訳では勿論ないのですが、今回はたまたま得られるデータが大文字のローマ字表記※1なので、実験的に非常に単純化した以下のような音素と素性との対応を想定してみます。
| A | I/Y | U/W | E | O | P | B | M | H | T | D | N | S | C | Z | R | K | G[g] | G[ŋ] | |
| consonantal | + | + | + | + | + | + | + | + | + | + | + | + | + | + | |||||
| sonorant | + | + | + | + | + | – | – | + | – | – | – | + | – | – | – | + | – | – | + |
| voiced | + | + | + | + | + | – | + | + | – | – | + | + | – | – | + | + | – | + | + |
| nasal | – | – | + | – | – | – | + | – | – | – | – | – | – | + | |||||
| contact | – | – | – | – | – | + | + | + | – | + | + | + | – | + | – | + | + | + | + |
| constriction | – | – | – | + | + | + | + | + | + | + | + | + | + | + | + | + | |||
| strident | – | – | – | – | – | – | – | – | – | – | – | – | + | + | + | – | – | – | – |
| high | – | + | + | – | – | + | + | + | – | + | + | + | |||||||
| low | + | – | – | – | – | – | – | – | + | – | – | – | – | – | – | – | – | ||
| palatal | – | + | – | + | – | – | – | – | – | – | – | – | – | + | – | – | – | – | – |
| grave | + | – | + | – | + | + | + | + | + | – | – | – | – | – | – | – | + | + | + |
| labial | + | + | + | + | + | – | – | – | – | – | – | – | – | – | – | – |
このとき、素性がネガティブ「ー」であるということとそもそもその素性をもたない「 」ということの違いをどのように数値に反映させるかが問題になると予想されますが、素性がポジティブ「+」であるという情報だけで今回の各ローマ字を互いに弁別することができるのでとりあえず「+」を1にそれ以外を0に変換してベクトル化してみることにします。例えばAは(0,1,1,0,0,0,0,0,1,0,1,0)に、Pは(1,0,0,0,1,1,0,1,0,0,1,1)になります。
このようにしてできたワンホットな音韻素性ベクトルの総和を各単語の素性ベクトル、Bag of Featuresとして扱うという訳です。例えばTOKAKEのBoFは以下のようになります。
TOKAKEの語形素性ベクトル
[ 3,3,3,0,3,3,0,2,1,1,4,1 ]
※1Gについては有声軟口蓋破裂音G[g]と有声軟口蓋鼻音G[ŋ]の二つがかき分けられていましたので、その点は反映させました。
※2単語を音韻素性ベクトルとして表現するというこの種のアイデアは全く新しいものというわけではなく、管見の限りでも(西川, 森田., 2021)のような研究が見つかりました。しかし、方言などの語形の分類にはあまり使われてこなかったようで、この記事の新規性はそこにあるかなと(ほっ)
結果
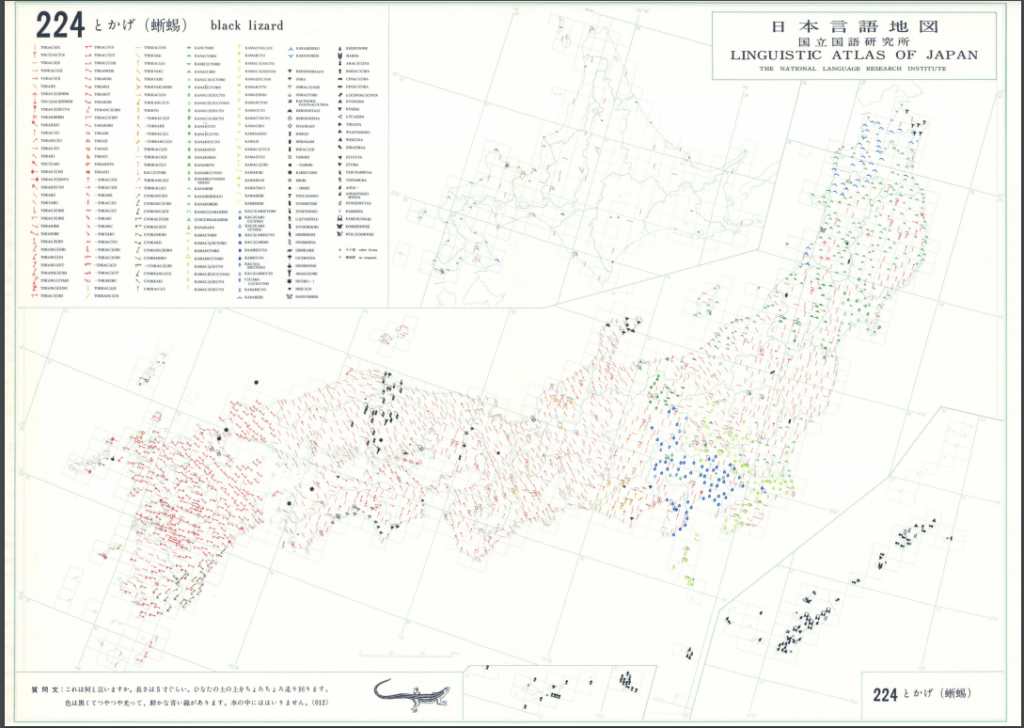
それでは実際に分類してみましょう。今回も例によって『日本言語地図』(LAJDB)データベースの「とかげ(蜥蜴)」のデータを利用しました。データの公開・管理、ほんとにいつもありがとうございます。クラスターの数は元の地図の分類に合わせて、無回答などをのぞいて8つとしました。
以下にBoCとBoFを用いた分類をそれぞれGoogle My Maps上に表示したものを示します※1。図5に示す元の地図(『日本言語地図 第5集』「とかげ(蜥蜴)」の分布図)と見比べてもらうと色による分類が大体対応していることが確認できると思います。今回の調査は2605回答にも及ぶ大規模なものですので、その回答の分類をこんなに簡単な方法でここまで再現できるというのはかなり魅力的ですね。もちろん、よく見ると回答数の少ない語形の分類は結構適当だったりするんですが、それでも「とかげ」「かなへび」「かなちょろ」「かがみっちょ」「かまぎっちょ」あたりの代表的な語形をきちんと別のクラスターに分類できているのは立派なものだと思います。
さて、ここまでで機械学習を使って語形を分類する方法の紹介自体は終わったので本稿の目的は達成された訳なんですが、せっかくなので今回提案したBoFにはどんなメリットがあるのか、BoCと比較して考察してみようと思います。
発展:BoCとBoFの比較
表3、表4はBoCを用いた場合とBoFを用いた場合それぞれの分類結果を各クラスターとその代表的な語形によって示したものです。「ラベル」には各クラスターの中で最も回答の多い語形を採用しました。「代表語形」には各クラスターの中から回答の多い順に選んだ3つの語形を示し、その他の語形も含めてそれぞれの語形の回答数を括弧内に示しています。またラベルの順番はどちらもアルファベット順としています。
| ラベル | 代表語形 |
| KAG[ŋ]AMIC(C)YO(O)類 (238) | KAG[ŋ]AMIC(C)YO(O)(54) KAMAG[g]IC(C)YO(O)(44) KANACYORO(16) その他(124) |
| KANAHEBI類 (298) | KANAHEBI(161) KARAHEBI(35) BAKAG[g]IRA(19) その他(83) |
| TOKAG[g]E類 (232) | TOKAG[g]E(214) ~~~TOKAG[g]E(6) KEEBYOOME(4) その他(8) |
| TOKAG[g]IRI類 (193) | TOKAG[g]IRI(75) TOKAG[g]I(25) TOKAG[g]II(23) その他(70) |
| TOKAG[ŋ]E類 (546) | TOKAG[ŋ]E(464) TOKAG[ŋ]I(36) ~~~TOKAG[ŋ]E(18) その他(28) |
| TOKAKE類 (648) | TOKAKE(544) TOKYAKU(30) TOKKAG[ŋ]E(21) その他(53) |
| TOKAKIRI類 (245) | TOKAKIRI(96) TOKAKI(81) TOKKAG[ŋ]I(11) その他(57) |
| Z(Y)OORIKIRI類 (82) | Z(Y)OORIKIRI(16) CYOKANG[g]IRI(11) CINAG[g]IRA(5) その他(50) |
| 無回答など※2 (123) | NR(109) 「その他」(14) |
| ラベル | 代表語形 |
| KAG[ŋ]AMIC(C)YO(O)類 (194) | KAG[ŋ]AMIC(C)YO(O)(54) KAMAG[g]IC(C)YO(O)(44) KANAG[g]IC(C)YO(16) その他(80) |
| KANAG[ŋ]IC(C)YO(O)類 (86) | KANAG[ŋ]IC(C)YO(O)(12) CYOKANG[g]IRI(11) KANEC(C)YORO(6) その他(57) |
| KANAHEBI類 (292) | KANAHEBI(161) KARAHEBI(35) BAKAG[g]IRA(19) その他(77) |
| TOKAG[ŋ]E類 (558) | TOKAG[ŋ]E(464) TOKAG[ŋ]I(36) ~~~TOKAG[ŋ]E(18) その他(40) |
| TOKAKE類 (908) | TOKAKE(544) TOKAG[g]E(214) TOKAKI(81) その他(69) |
| TOKAKIRI類 (269) | TOKAKIRI(96) TOKAG[g]IRI(75) TOKAG[g]II(23) その他(75) |
| TOKYAKU類 (120) | TOKYAKU(30) TOKKAG[ŋ]E(21) TOKAG[g]IT(20) その他(49) |
| Z(Y)OORIKIRI類 (55) | Z(Y)OORIKIRI(16) YOCUASI(KO)(6) ZYOOTO(OSI)(4) その他(29) |
| 無回答など※2 (123) | NR(109) 「その他」(14) |
さてさて、これを一体どのような観点で比較したらよいのか、正直まだ考えあぐねていますが、いくつか簡単に目につく相違点だけを見てもBoFのメリットが確認できます。
まずBoCを用いた分類では「TOKAKE」「TOKAG[g]E」「TOKAG[ŋ]E」がすべて別のクラスターに分類されているのに対し、BoFでは「TOKAKE」と「TOKAG[g]E」は同じクラスターに「TOKAG[ŋ]E」のみが別のクラスターに分類されています。これはBoCではKとG[g]とG[ŋ]を単に別のアルファベットとしてそれぞれの(非)類似度を全く同一のものとして扱ってしまうのに対し、BoFではK[k]とG[g]のほうがK[k]とG[ŋ]よりも多くの素性を共有しているとしてそれぞれの(非)類似度の差をよりよく表現するからだと考えられます。
また、BoCを用いた分類では「TOKAKIRI」と「TOKAG[g]IRI」とがそれぞれ別のクラスター、「TOKAKIRI類」と「TOKAG[g]IRI類」に分類されていますが、BoFではどちらも同じクラスター、「TOKAKIRI類」に分類されています。こえもBoCでは捉えられない[k]と[g]の音韻素性レベルの類似性をBoFは捉えられているからだと考えられます。
このようなBoFの強みがデータに拠らず発揮されるのかどうかは、今回扱った「とかげ」以外にも色んなデータを試してみる必要がありますが、BoFにはBoFの特有の強みがあるということは言えそうです。
※1経緯度情報付きの言語データをGoogle My Maps上に表示する方法はぜひ第2回の記事を参照ください。
※2無回答など(NRとその他)については予めデータを分けて手動でラベルを与えました。
終わりに
今回は機会学習で語形の分類を自動化する方法を共有しました。方法論の解説が思いの外長くなってしまったので、GoogleColaboratoryを使った具体的な実装の手順は稿を改めてご紹介しようと思います。
加えて、今回は語形のベクトル化の方法としてBoCの紹介をしたあと、音韻素性レベルの類似性を参照できるような改善案としてBoFを提案しました。まだまだ評価の方法には迷っていますが、どうやらBoFにはBoF特有の強みがあるということは確かなようです。今後も色々にテストを考えてみたいと思います。
最後に、今回扱ったK平均法ですが、分類の結果が1回目のランダムなクラスタリングに依存するため、試行のごとに結果が微妙に変わるというデメリットがあります。また、今回はクラスターの数を元の地図の分類に習いましたが、その根拠は厳密にいうとブラックボックスです。データのばらつきから適切なクラスター数を推定できるともっと良いなと思います。実はこのようなK平均法のデメリットを克服するアイデアは様々に提案されいます(G平均法、X平均法など)。今度はこのようなK平均法の拡張アルゴリズムを使って色々やってみたいなと思います。
是非是非、次回もお読みください。
参考文献
近藤泰弘(2023)「単語音素のベクトル化による言語地図作成」『言語処理学会 第29回年次大会 発表論文集』https://www.anlp.jp/proceedings/annual_meeting/2023/pdf_dir/B10-2.pdf
西川純平, 森田 純哉(2021)「音韻意識形成過程における誤りの認知モデリング」『ヒューマンインタフェース学会論文誌』23(2); 189-200
https://doi.org/10.11184/his.23.2_189
Chire. (2017, 5, 30). File:K-means convergence.gif – Wikipedia. https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:K-means_convergence.gif
使用したデータ
『日本言語地図』(LAJDB)データベースのデータを利用しました。データの管理・公開に感謝いたします。